Symmetry

L.O – To be able to find the number of lines of symmetry and the order of rotational symmetry for a wide range of shapes

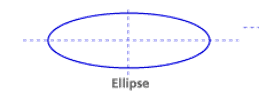
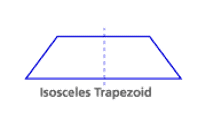
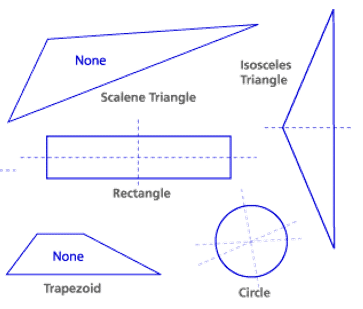
Line Symmetry :

A line of symmetry divides the shape into two equal parts.

Each part is a reflection of the other.

If a shape is folded along it’s line of symmetry each part fits exactly on top of the other.

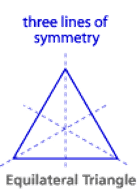
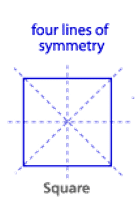
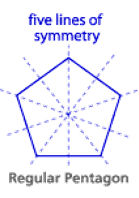
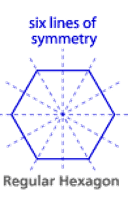
Remember, a regular polygon has the same number of lines of symmetry as it has sides

Rotaional Symmetry :

This is where you can rotate the shape into different positions that all look the same

A shape has rotational symmetry if it fits on top of itself more than once as it makes a complete turn.

The order of rotational symmetry is the number of times that the shape fits on 
top of itself. This must be 2 or more.

The “centre of rotation” is the point about which the shape turns.

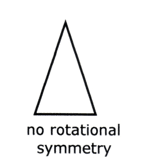
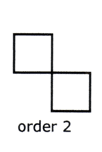
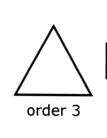
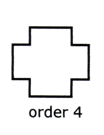
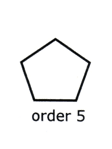
Remember, a regular polygon has the same order of rotational symmetry as it has sides.

Questions :

Draw all the lines of symmetry onto these shapes and write down the order of rotational symmetry.

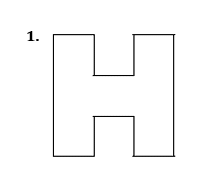
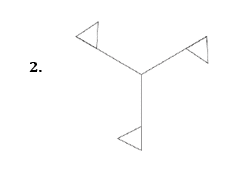
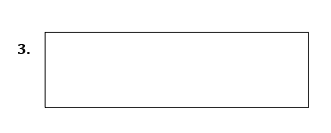
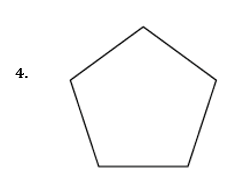
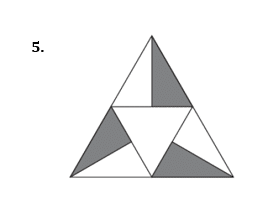
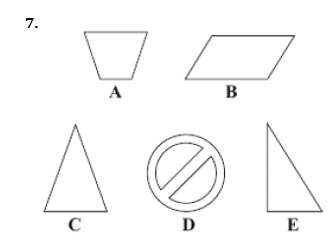
Pick out the shapes with

• only one line of symmetry
• rotational symmetry of order 2

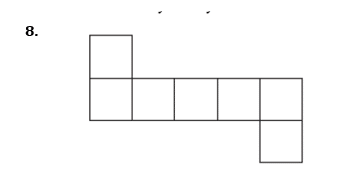
Mark with a cross the centre of rotation.

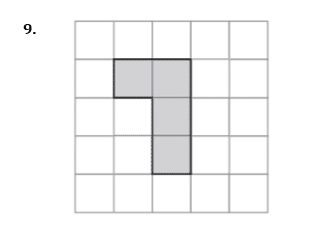
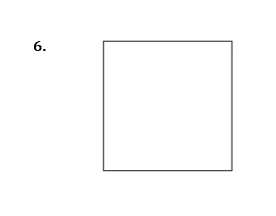
Shade one more square to make a pattern with one line of symmetry

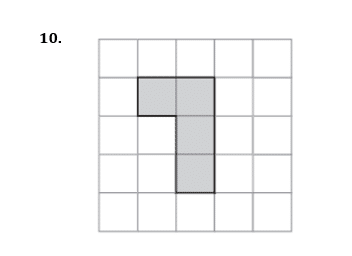
Shade one more square to make a pattern with

rotational symmetry of order 2