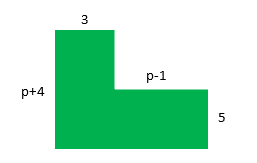Table of Contents
Unit 1 | Algebra
Page 1 | Expressions and Formulae
Page 3| Solving Linear Equations
Page 4| Expanding and Factorising
Page 5| Factorising Quadratics and expanding double brackets
Page 6| Patterns and Sequences
Page 7| Simultaneous Equations
Page 8| Changing the subject of a Formula
Page 9| Adding , subtracting algebraic formulas
Unit 2 |Graphs
Page 1 | Straight line graphs
Page 2 | Graphs of Quadratic functions
Unit 3 |Geometry and Measure
Page 2 | Symmetry
Page 3 | Coordinates
Page 4 | Perimeter, Area, Volume
Page 6 | Measurement
Page 7 | Trigonometry
Page 8 | Pythagoras
Page 9 | Angles
Page 10 | Shapes
Page 11| Time
Page 12 | Locus
Unit 4 | Numbers
Page 1 | Speed, Distance and time
Page 2 | Rounding and estimating
Page 3 | Ratio and proportion
Page 4 | Factors, Multiples and primes
Page 5 | Powers and roots
Page 7 | Positive and negative numbers
Page 8 | Basic operations
Page 9 | Fractions
Page 10 | Percentages
Unit 5 | Statistics and Probability
Page 1 | Sampling data (MA)
Page 2 | Recording and representing data
Page 3 | Mean median range and mode
Page 4 | Standard deviation
Unit 4 | Calculus
Solving Linear Equations
L.O To be able to use inverse operations to solve algebraic expressions
Equations always include an equals sign so then there are two parts to the expression. The key to solving equations is balancing out both sides which usually involves making the algebraic term the subject.
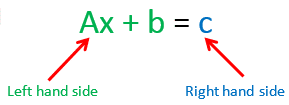

Example 1: Solve the equation 2s + 1 = 29
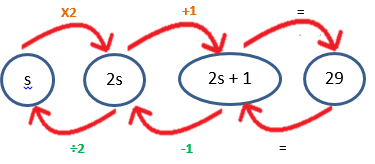
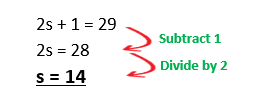



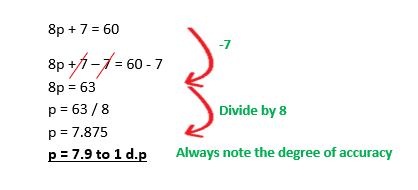
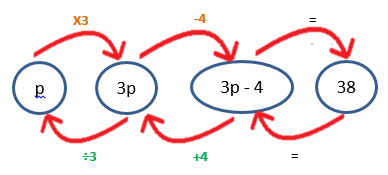
Example 2: Solve the equation 3p – 4 = 38
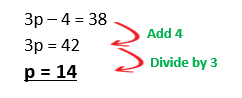



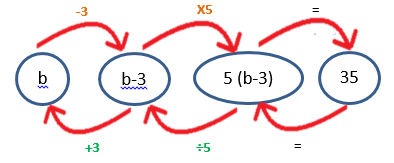
Example 3: Solve the equation 5 (b – 3 ) = 35
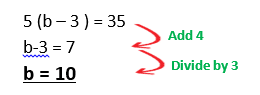



However there is also an alternative and quicker way of answering this question:
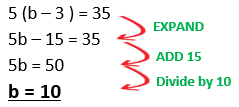

Example 4: Solve the equation 7 – 8x = 15
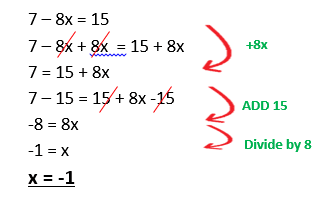



Example 5: Solve the equation 7 – a = 3a + 5




Word Problems
Sometimes you will have to write the expression itself before you solve it.
a) John thinks of a number. He multiplies the number 9 then subtracts 6 from that total. If he is left with 21, which number did John initially think of?
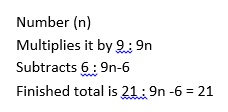
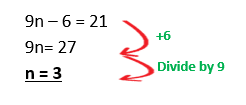

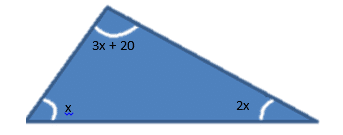
b)A triangle has the angles 3x +20 , x and 2x. Samantha wants to work out the value of x in this triangle.
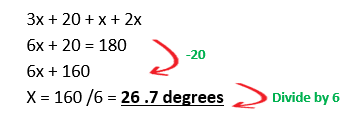


![]()
c) Amelia is x years old. Her brother Bailey is 6 years older than her. Amelia’s mum is 3 times the age of bailey and Amelia’s father is 5 years younger than Amelia’s mum. Write separate expressions for the ages of Amelia, Bailey, mum and dad in terms of Amelia’s age.
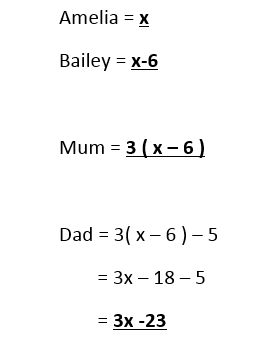




d) Using the information from the question above. If Amelia’s mum is 45 years old then how old is each member of the family age.
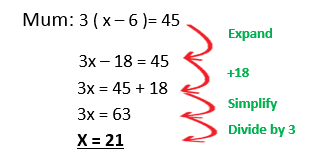
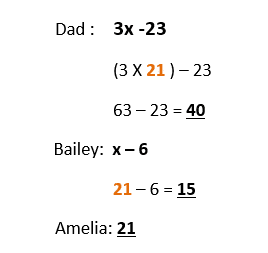


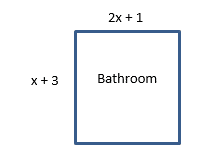
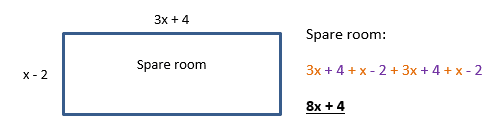
e) Aadil has moved into his university apartment. He found some blue prints of the bathroom and a spare room in the house (diagram below). He has a lot of furniture to fit in so worked out the perimeter of each room. If the perimeters of each room are the same what is the area of the bathroom?


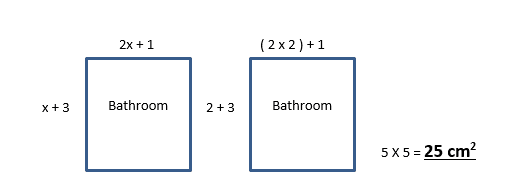
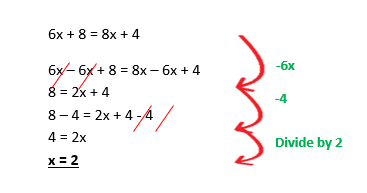




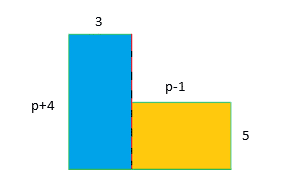
f) Amina’s Lawn is pictured on the side. She wanted to apply some fresh soil to the lawn and worked out that the area was 60cm2. However after applying the soil she notices foxes and rabbits burrowing into the lawn so decides to put up a fence along the full perimeter of the lawn. If a fence cost £2.50 per cm, how much will a full fence for her lawn cost?