Table of Contents
Unit 1 | Algebra
Page 1 | Expressions and Formulae
Page 3| Solving Linear Equations
Page 4| Expanding and Factorising
Page 5| Factorising Quadratics and expanding double brackets
Page 6| Patterns and Sequences
Page 7| Simultaneous Equations
Page 8| Changing the subject of a Formula
Page 9| Adding , subtracting algebraic formulas
Unit 2 |Graphs
Page 1 | Straight line graphs
Page 2 | Graphs of Quadratic functions
Unit 3 |Geometry and Measure
Page 2 | Symmetry
Page 3 | Coordinates
Page 4 | Perimeter, Area, Volume
Page 6 | Measurement
Page 7 | Trigonometry
Page 8 | Pythagoras
Page 9 | Angles
Page 10 | Shapes
Page 11| Time
Page 12 | Locus
Unit 4 | Numbers
Page 1 | Speed, Distance and time
Page 2 | Rounding and estimating
Page 3 | Ratio and proportion
Page 4 | Factors, Multiples and primes
Page 5 | Powers and roots
Page 7 | Positive and negative numbers
Page 8 | Basic operations
Page 9 | Fractions
Page 10 | Percentages
Unit 5 | Statistics and Probability
Page 1 | Sampling data (MA)
Page 2 | Recording and representing data
Page 3 | Mean median range and mode
Page 4 | Standard deviation
Unit 4 | Calculus
Factors, Multiples and Primes
L.O – To be able to find the multiples, factors and prime factors of numbers. Also, be able to find the LCM and HCF of numbers.
Multiples
The multiples of a number are its times table.
For example, the multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 etc
11 are 11, 22, 33, 44, 55, 66 etc
25 are 25, 50, 75, 100, 125 etc
Factors
The factors of a number are all the numbers that divide into it (without remainders).
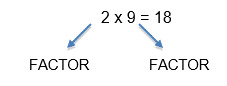
So, 2 and 9 are factors of 18. However 18 has many more factors including 3, 6 etc
By following the method below, you will be sure to find all the factors of a number.
Example 1:
Find the factors of 12
1. Draw a box in which you will insert all the factors. Write down 1at the front and 12 at the end
 2.Work onwards from one to 2, 3, 4, 5, etc and see if these numbers divide into the number given in the question
2.Work onwards from one to 2, 3, 4, 5, etc and see if these numbers divide into the number given in the question
– The next number is 2
2 x 6 = 12, so 2 and 6 are factors

The next number is 3
3 x 4 = 12

The next number is 4.
However we have already put 4 into the table. So this is where we stop
Steps:
- Draw a box. Put the number 1 at the front and the number given in the question at the end. These are the first pair of factors
- Work onwards from 1 to 2, 3, 4, 5 etc
- The next number is 2. See if 2 divides into the number given in the If it does put 2 in the next box at the beginning and its corresponding factor at the end.
E.g. if the number in the question was 12à 2 x 6 = 12
- The next number is 3. Repeat the same steps as above.
- Not all numbers will divide into the number in the question. If this is the case do not insert this into the table. Then move onto the next number
- Eventually a factor will be repeated. This is when you stop.
See the example above in order to understand these steps!
Prime Factors
Remember a prime number are numbers that don’t divide by anything apart from 1 and themselves. Examples include 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 etc
In order the find the prime factors of a number, you must draw out a factor tree.
Example 1:
Find the prime factors of 210
– Start off with 210. Start ‘splitting the number up’ (this can be done in many ways).
– Then split the numbers again
– Once you reach prime numbers – put a circle around them/highlight them. These cannot be split anymore and are the prime factors.
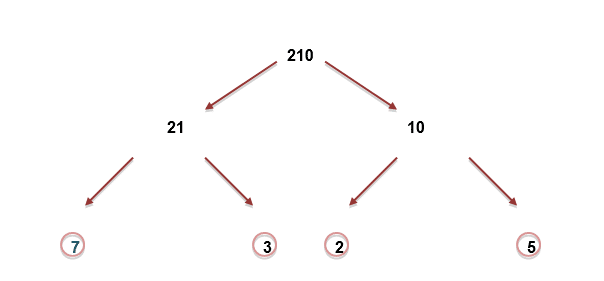
The prime factors of 210 are 2, 3, 5 and 7
So, 210 expressed as a product of its prime factors = 2 x 3 x 5 x 7
In an exam, always write the numbers multiplied by one another
The steps are shown above for this type of question. Just remember to keep splitting the numbers up until you can’t split any futher!
LCM – Lowest Common Multiple
The lowest common multiple is the smallest positive number that is a multiple of two or more numbers i.e. it will divide by all the numbers in the question
In order to find the lowest common multiple you need to lists the multiples of the numbers in the question and find the smallest multiple which appears in all the lists.
Example 1:
Find the lowest common multiple (LCM) of 6 and 8.
- Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, 48, 54, 60….
Multiples of 8 = 8, 16, 24, 32, 40, 48, 56, 64, 72, 80….
- The smallest multiple that appears in both lists is 24
Therefore, the LCM of 6 and 8 is 24.
Steps:
- List the multiples of the numbers in the question i.e. write out their times tables.
Writeout 10 multiples to begin with, however you may need to go further into the times table if needed.
- Look at the lists you just wrote out. Find the smallest number which appears in both lists.
This is the lowest common multiple.
HCF – Highest Common Factor
The highest common factor is the largest positive number which will divide into all the numbers in the question, without any remainders.
In order to find the highest common factor of numbers, you need to list the factors of all the numbers in the question. Then, find the largest factor which appears in all the lists.
Example 1:
Find the highest common factor (HCF) of 36 and 90
- Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 90 = 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
- The largest factor which appears in both lists is 18.
Therefore, the HCF of 36 and 90 is 18.
Steps:
- List all the factors of the numbers in the question.
You can do this using the method shown above under ‘Factors’
- Look at the lists you just wrote out. Find the largest number which appears in both lists.
This is the highest common factor (HCF).
Find the first 10 multiples of the following numbers
- 13
- 6
- 9
- 12
Find the prime factors of the following numbers. Give the answer as a product of prime factors
- 160
- 36
- 40
- 660
Find the HCF of the followingnumbers
- 72 and 96
- 128 and 320
- 48 and 84
- 45 and 27
- 24, 36 and 18
Find all the factors of the following numbers
- 35
- 64
- 84
- 13
Find the LCM of the following numbers
- 32 and 40
- 12 and 18
- 12 and 5
- 7 and 9
- 3, 6 and 7


